بيان موجه خال من الحلقات

يرجى إضافة وصلات داخلية للمقالات المتعلّقة بموضوع المقالة.
يرجى إضافة قالب معلومات متعلّقة بموضوع المقالة.
يرجى مراجعة هذه المقالة وإزالة وسم المقالات غير المراجعة، ووسمها بوسوم الصيانة المناسبة.
من ويكيبيديا، الموسوعة الحرة
ترتيب طوبولوجي للرسم البياني غير الدوري الموجه: تنتقل كل حافة من الترتيب السابق (أعلى اليسار) إلى الترتيب المتأخر (أسفل اليمين). يكون الرسم البياني الموجه غير دوري إذا وفقط إذا كان يحتوي على ترتيب طوبولوجي..

البيان الموجه الخالي من الحلقات[1] (بالإنجليزية: Directed acyclic graph)‏، في الرياضيات، ولا سيما نظرية الرسم البياني وعلوم الكمبيوتر، الرسم البياني غير الدوري الموجه (DAG أو dag / ˈdæɡ / (حول هذا الصوت)) هو رسم بياني موجه بدون دورات موجهة. أي أنه يتكون من الرؤوس والحواف (تسمى أيضًا الأقواس)، مع توجيه كل حافة من رأس إلى آخر، بحيث لا توجد طريقة للبدء من أي قمة v واتباع تسلسل متسق من الحواف التي تتكرر في النهاية ل v مرة أخرى. بالتساوي، DAG هو رسم بياني موجه له ترتيب طوبولوجي، تسلسل من القمم بحيث يتم توجيه كل حافة من وقت سابق إلى لاحقًا في التسلسل.

يمكن لـ DAGs نمذجة العديد من أنواع المعلومات المختلفة. على سبيل المثال، يمكن نمذجة جدول بيانات على هيئة DAG ، برأس لكل خلية وحافة عندما تستخدم الصيغة في خلية واحدة القيمة من أخرى؛ يمكن استخدام الترتيب الطوبولوجي لـ DAG هذا لتحديث جميع قيم الخلايا عند تغيير جدول البيانات. وبالمثل، يمكن استخدام الترتيب الطوبولوجي لـ DAGs لطلب عمليات التجميع في ملف makefile. تستخدم تقنية تقييم البرنامج ومراجعته (PERT) DAGs لنمذجة معالم وأنشطة المشاريع البشرية الكبيرة، وجدولة هذه المشاريع لاستخدام أقل وقت إجمالي ممكن. تتضمن الكتل المنطقية التوافقية في تصميم الدوائر الإلكترونية، والعمليات في لغات برمجة تدفق البيانات، شبكات غير دورية لعناصر المعالجة. يمكن أن تمثل DAG أيضًا مجموعات من الأحداث وتأثيرها على بعضها البعض، إما في بنية احتمالية مثل شبكة Bayesian أو كسجل للبيانات التاريخية مثل أشجار العائلة أو تواريخ الإصدارات لأنظمة التحكم في المراجعة الموزعة. يمكن أيضًا استخدام DAGs كتمثيل مضغوط لبيانات التسلسل، مثل تمثيل الرسم البياني للكلمات الحلقية الموجه لمجموعة من السلاسل، أو تمثيل مخطط القرار الثنائي لتسلسل الخيارات الثنائية. بشكل أكثر تجريدًا، تشكل علاقة قابلية الوصول في DAG ترتيبًا جزئيًا، ويمكن تمثيل أي ترتيب جزئي محدود بواسطة DAG باستخدام قابلية الوصول.

تتضمن المشكلات الحسابية ذات الوقت متعدد الحدود المهمة في DAGs الفرز الطوبولوجي (حساب الترتيب الطوبولوجي)، وبناء الإغلاق الانتقالي والاختزال الانتقالي (أكبر وأصغر DAGs مع نفس علاقة قابلية الوصول، على التوالي) للمجموعات، ومشكلة الإغلاق، حيث الهدف هو العثور على مجموعة فرعية ذات وزن أدنى من الرؤوس بدون حواف تربطها ببقية الرسم البياني. يعد تحويل الرسم البياني الموجه بالدورات إلى DAG عن طريق حذف أقل عدد ممكن من الرؤوس أو الحواف (مجموعة قمة التغذية المرتدة ومشكلة مجموعة حافة التغذية المرتدة، على التوالي) مشكلة صعبة NP ، ولكن يمكن تحويل أي رسم بياني موجه إلى DAG (التكثيف) عن طريق التعاقد مع كل مكون متصل بقوة في خفة واحدة. يمكن حل مشاكل العثور على أقصر المسارات والمسارات الأطول على DAGs في الوقت الخطي، على عكس الرسوم البيانية التعسفية التي تكون فيها خوارزميات المسار الأقصر أبطأ وأطول مسار مشاكل NP-hard.

المفهوم المقابل للرسوم البيانية غير الموجهة هو الغابة، رسم بياني غير موجه بدون دورات. ينتج عن اختيار اتجاه الغابة نوعًا خاصًا من الرسم البياني غير الدوري الموجه يسمى الشجرة المتعددة. ومع ذلك، لا يتوافق كل رسم بياني غير دوري موجه مع اتجاه حواف رسم بياني لا دوري غير موجه. بعد كل شيء، كل رسم بياني غير موجه، سواء كان دوريًا أو غير دوري، له اتجاه لا دوري، وتخصيص لاتجاه لحوافه يجعله في رسم بياني لا دوري موجه. للتأكيد على أن DAGs ليست هي نفس الإصدارات الموجهة من الرسوم البيانية غير الدورية غير الموجهة، يسميها بعض المؤلفين الرسوم البيانية غير الدورية الموجهة [1] أو الرسوم البيانية غير الدورية.

التعاريف[عدل]

يتكون الرسم البياني من الرؤوس والحواف التي تربط أزواج الرؤوس، حيث يمكن أن تكون الرؤوس أي نوع من الكائنات المتصلة في أزواج من خلال الحواف. في حالة الرسم البياني الموجه، يكون لكل حافة اتجاه، من قمة إلى أخرى. المسار في الرسم البياني الموجه هو سلسلة من الحواف لها خاصية أن رأس النهاية لكل حافة في التسلسل هو نفس رأس البداية للحافة التالية في التسلسل؛ يشكل المسار دورة إذا كانت قمة البداية للحافة الأولى تساوي رأس النهاية للحافة الأخيرة. الرسم البياني غير الدوري الموجه هو رسم بياني موجه ليس له دورات.[2][3][4]

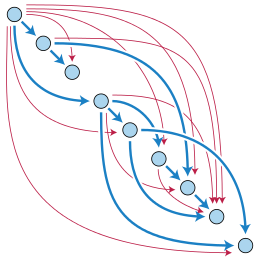
تؤدي إضافة الحواف الحمراء إلى الرسم البياني غير الدوري الموجه باللون الأزرق إلى إنتاج DAG آخر ، وهو الإغلاق الانتقالي للرسم البياني الأزرق. لكل حافة حمراء أو زرقاء uv ، يمكن الوصول إلى v من u: يوجد مسار أزرق يبدأ من u وينتهي عند v.}}.

تؤدي إضافة الحواف الحمراء إلى الرسم البياني غير الدوري الموجه باللون الأزرق إلى إنتاج DAG آخر، وهو الإغلاق الانتقالي للرسم البياني الأزرق. لكل حافة حمراء أو زرقاء uv ، يمكن الوصول إلى v من u: يوجد مسار أزرق يبدأ من u وينتهي عند v. يُقال إن الرأس v للرسم البياني الموجه يمكن الوصول إليه من قمة أخرى u عندما يكون هناك مسار يبدأ من u وينتهي عند v. كحالة خاصة، يُعتبر كل رأس يمكن الوصول إليه من نفسه (عن طريق مسار بصفر حواف). إذا كان بإمكان الرأس الوصول إلى نفسه عبر مسار غير بديهي (مسار به حافة واحدة أو أكثر)، فإن هذا المسار عبارة عن دورة، لذلك هناك طريقة أخرى لتحديد الرسوم البيانية الحلقية الموجهة وهي أنها الرسوم البيانية التي لا يمكن أن يصل فيها أي رأس إلى نفسه عبر مسار غير بديهي.[5]

الترتيب الطوبولوجي للرسم البياني الموجه هو ترتيب رؤوسه في تسلسل، بحيث يحدث رأس بداية الحافة لكل حافة في وقت أبكر في التسلسل من قمة نهاية الحافة. لا يمكن أن يحتوي الرسم البياني الذي يحتوي على ترتيب طوبولوجي على أي دورات، لأنه يجب توجيه الحافة في الرأس الأول للدورة بطريقة خاطئة. لذلك، كل رسم بياني بترتيب طوبولوجي لا دوري. على العكس من ذلك، يحتوي كل رسم بياني لا دوري موجه على ترتيب طوبولوجي واحد على الأقل. لذلك، يمكن استخدام هذه الخاصية كتعريف بديل للرسومات البيانية الحلقية الموجهة: فهي بالضبط الرسوم البيانية التي لها ترتيب طوبولوجي.

الخصائص الرياضية[عدل]

قابلية الوصول، الإغلاق المتعدي، والاختزال المتعدي

يمكن صياغة علاقة قابلية الوصول في أي رسم بياني لا دوري موجه كترتيب جزئي as على رؤوس DAG. في هذا الترتيب الجزئي، يتم ترتيب رأسين u و v على شكل u ≤ v تمامًا عندما يكون هناك مسار موجه من u إلى v في DAG ؛ أي عندما يمكن الوصول إلى v من u. [5] ومع ذلك، قد تؤدي DAGs المختلفة إلى نفس علاقة قابلية الوصول ونفس الترتيب الجزئي. [6] على سبيل المثال، DAG ذات الحافتين a → b و b → c لها نفس علاقة قابلية الوصول مثل الرسم البياني بثلاثة حواف a → b و b → c و a → c. كل من DAGS هذه تنتج نفس الترتيب الجزئي، حيث يتم ترتيب الرؤوس على أنها a a b c.

إذا كانت G عبارة عن DAG ، فإن إغلاقها الانتقالي هو الرسم البياني الذي يحتوي على معظم الحواف التي تمثل نفس علاقة قابلية الوصول. لها حافة u → v كلما تمكنت من الوصول إلى v. أي أنها تتمتع بميزة لكل زوج u ≤ v ذي صلة من العناصر المميزة في علاقة قابلية الوصول لـ G ، وبالتالي يمكن اعتبارها ترجمة مباشرة لقابلية الوصول العلاقة ≤ في المصطلحات النظرية للرسم البياني. تعمل نفس طريقة ترجمة الطلبات الجزئية إلى DAGs بشكل عام: لكل مجموعة محدودة مرتبة جزئيًا (S ، ≤)، يكون الرسم البياني الذي يحتوي على رأس لكل عضو من S وحافة لكل زوج من العناصر المرتبطة بـ u ≤ v هو تلقائيًا DAG مغلق مؤقتًا، وله (S ، ≤) كعلاقة قابلية الوصول. وبهذه الطريقة، يمكن تمثيل كل مجموعة محدودة مرتبة جزئيًا كعلاقة قابلية الوصول لـ DAG.

التخفيض الانتقالي لـ DAG G هو الرسم البياني ذو الحواف الأقل التي تمثل نفس علاقة قابلية الوصول مثل G. إنه رسم فرعي لـ G ، يتشكل من تجاهل الحواف u → v التي يحتوي G أيضًا على مسار أطول يربط نفس الاثنين الرؤوس. مثل الإغلاق المتعدي، يتم تعريف الاختزال الانتقالي بشكل فريد لـ DAGs. في المقابل، بالنسبة للرسم البياني الموجه الذي لا يكون غير دوري، يمكن أن يكون هناك أكثر من رسم بياني فرعي أدنى واحد له نفس علاقة قابلية الوصول.[6]

يمثل مخطط Hasse الترتيب الجزئي لتضمين المجموعة (⊆) بين المجموعات الفرعية لمجموعة من ثلاثة عناصر..

يمثل مخطط Hasse الترتيب الجزئي لتضمين المجموعة (⊆) بين المجموعات الفرعية لمجموعة من ثلاثة عناصر. إذا كانت DAG G لها علاقة قابلية الوصول الموصوفة بالترتيب الجزئي ≤ ، فإن التخفيض الانتقالي لـ G هو رسم بياني فرعي لـ G له حافة u → v لكل زوج في علاقة التغطية ≤. تعتبر التخفيضات الانتقالية مفيدة في تصور الطلبات الجزئية التي تمثلها، لأنها تحتوي على حواف أقل من الرسوم البيانية الأخرى التي تمثل نفس الطلبات وبالتالي تؤدي إلى رسومات بيانية أبسط. مخطط Hasse للترتيب الجزئي هو رسم للتصغير الانتقالي حيث يتم عرض اتجاه كل حافة بوضع رأس البداية للحافة في موضع أدنى من رأس النهاية.[7]

الترتيب الطوبولوجي

يحتوي كل رسم بياني لا دوري موجه على ترتيب طوبولوجي، وهو ترتيب للرؤوس بحيث تظهر نقطة نهاية كل حافة في وقت مبكر في الترتيب عن نقطة نهاية الحافة. يمكن استخدام وجود مثل هذا الترتيب لتوصيف DAGs: الرسم البياني الموجه هو DAG إذا وفقط إذا كان يحتوي على ترتيب طوبولوجي. بشكل عام، هذا الترتيب ليس فريدًا؛ يحتوي DAG على ترتيب طوبولوجي فريد إذا وفقط إذا كان يحتوي على مسار موجه يحتوي على جميع الرؤوس، وفي هذه الحالة يكون الترتيب هو نفسه الترتيب الذي تظهر به الرؤوس في المسار.

عائلة الترتيب الطوبولوجي لـ DAG هي نفس عائلة الامتدادات الخطية لعلاقة قابلية الوصول لـ DAG ، لذا فإن أي رسمين بيانيين يمثلان نفس الترتيب الجزئي لهما نفس مجموعة الأوامر الطوبولوجية.[8]

العد التجميعي

تمت دراسة مشكلة تعداد الرسم البياني لعد الرسوم البيانية غير الحلقية الموجهة بواسطة Robinson (1973). عدد DAGs على رؤوس n المسمى، لـ n = 0، 1، 2، 3... (بدون قيود على الترتيب الذي تظهر به هذه الأرقام في الترتيب الطوبولوجي لـ DAG) هو

1، 1، 3، 25، 543، 29281، 3781503... (تسلسل A003024 في OEIS). يمكن حساب هذه الأرقام من خلال علاقة التكرار

تخمين إريك دبليو وايسشتاين، [9] وماكي وآخرون. (2004) أثبت أن نفس الأرقام تحسب المصفوفات (0,1) التي تكون جميع القيم الذاتية لها أرقامًا حقيقية موجبة. البرهان حيوي: المصفوفة A هي مصفوفة مجاورة لـ DAG إذا وفقط إذا كانت A + I مصفوفة (0,1) مع جميع القيم الذاتية موجبة، حيث أنا أشير إلى مصفوفة الهوية. نظرًا لأن DAG لا يمكن أن تحتوي على حلقات ذاتية، يجب أن تحتوي مصفوفة تجاورها على صفر قطري، لذا فإن إضافة I تحافظ على خاصية أن جميع معاملات المصفوفة هي 0 أو 1.[10]

عائلات الرسوم البيانية ذات الصلة

الشجرة القطبية عبارة عن رسم بياني موجه يتكون من توجيه حواف الشجرة الحرة.[11] كل شجرة قطب هي DAG. على وجه الخصوص، هذا صحيح بالنسبة للأشجار التي تشكلت عن طريق توجيه جميع الحواف للخارج من جذور الشجرة.

الشجرة المتعددة (تسمى أيضًا الرسم البياني الذي لا لبس فيه أو المنغروف) هي رسم بياني موجه يوجد فيه على الأكثر مسارًا موجهًا واحدًا (في أي اتجاه) بين أي رأسين؛ بشكل مكافئ، هو DAG حيث، لكل رأس v ، يكون الرسم البياني الفرعي الذي يمكن الوصول إليه من v يشكل شجرة.[12]

مشاكل حسابية[عدل]

الفرز والاعتراف الطوبولوجي

الفرز الطوبولوجي هو مشكلة الخوارزمية لإيجاد ترتيب طوبولوجي لـ DAG معين. يمكن حلها في الوقت الخطي. تقوم خوارزمية Kahn للفرز الطوبولوجي ببناء ترتيب قمة الرأس مباشرة. يحتفظ بقائمة من الرؤوس التي ليس لها حواف واردة من رؤوس أخرى لم يتم تضمينها بالفعل في الترتيب الطوبولوجي المركب جزئيًا؛ تتكون هذه القائمة في البداية من الرؤوس التي لا تحتوي على حواف واردة على الإطلاق. بعد ذلك، تضيف بشكل متكرر رأسًا واحدًا من هذه القائمة إلى نهاية الترتيب الطوبولوجي المركب جزئيًا، وتتحقق مما إذا كان يجب إضافة جيرانها إلى القائمة. تنتهي الخوارزمية عندما تتم معالجة جميع الرؤوس بهذه الطريقة. بدلاً من ذلك، يمكن إنشاء ترتيب طوبولوجي عن طريق عكس ترقيم الطلب اللاحق لمسح الرسم البياني للبحث العمق أولاً.

من الممكن أيضًا التحقق مما إذا كان الرسم البياني الموجه هو DAG في الوقت الخطي، إما عن طريق محاولة العثور على ترتيب طوبولوجي ثم اختبار لكل حافة ما إذا كان الترتيب الناتج صالحًا أو بدلاً من ذلك، بالنسبة لبعض خوارزميات الفرز الطوبولوجي، من خلال التحقق من أن الخوارزمية تطلب جميع القمم بنجاح دون تلبية شرط الخطأ.[13]

البناء من الرسوم البيانية الدورية

يمكن تحويل أي رسم بياني غير موجه إلى DAG باختيار ترتيب إجمالي لرؤوسه وتوجيه كل حافة من نقطة النهاية السابقة بالترتيب إلى نقطة النهاية اللاحقة. يسمى الاتجاه الناتج للحواف اتجاه لا دوري. قد تؤدي الطلبات الإجمالية المختلفة إلى نفس الاتجاه غير الدوري، لذلك يمكن أن يكون للرسم البياني n-vertex أقل من n! التوجهات غير الدورية. عدد الاتجاهات غير الدورية يساوي | χ (−1) | ، حيث χ هي كثير الحدود اللوني للرسم البياني المعطى.

الرسم البياني غير الدوري الموجه باللون الأصفر هو تكثيف الرسم البياني الأزرق الموجه. يتم تشكيله عن طريق التعاقد مع كل مكون متصل بقوة من الرسم البياني الأزرق في رأس أصفر واحد..

إغلاق انتقالي واختزال متعد

يمكن إنشاء الإغلاق الانتقالي لـ DAG معين، برؤوس n وحواف m ، في الوقت O (mn) باستخدام إما بحث العرض أولاً أو بحث العمق أولاً لاختبار إمكانية الوصول من كل قمة. [22] بدلاً من ذلك، يمكن حلها في الوقت O (nω) حيث ω <2.373 هي الأس لخوارزميات مضاعفة المصفوفة السريعة؛ هذا تحسن نظري على O (mn) المرتبط بالرسوم البيانية الكثيفة.

في كل خوارزميات الإغلاق المتعدية هذه، من الممكن التمييز بين أزواج الرؤوس التي يمكن الوصول إليها من خلال مسار واحد على الأقل بطول اثنين أو أكثر من الأزواج التي لا يمكن توصيلها إلا بمسار طوله واحد. يتكون الاختزال المتعدي من الحواف التي تشكل مسارات بطول واحد وهي المسارات الوحيدة التي تربط نقاط النهاية الخاصة بها. لذلك، يمكن بناء الاختزال المتعدي في نفس الحدود الزمنية التقاربية مثل الإغلاق المتعدي.

مشكلة الإغلاق

تأخذ مشكلة الإغلاق كمدخل رسمًا بيانيًا دائريًا موجهًا مرجحًا للرأس وتبحث عن الحد الأدنى (أو الأقصى) لوزن الإغلاق - مجموعة من الرؤوس C ، بحيث لا تترك أي حواف C. لا دورية، ولكن بدون عمومية أكبر، لأنها في هذه الحالة تعادل نفس المشكلة في تكثيف الرسم البياني. يمكن حلها في زمن كثير الحدود باستخدام تقليل مشكلة التدفق الأقصى.[14]

خوارزميات المسار

تصبح بعض الخوارزميات أبسط عند استخدامها على DAGs بدلاً من الرسوم البيانية العامة، بناءً على مبدأ الترتيب الطوبولوجي. على سبيل المثال، من الممكن العثور على أقصر المسارات والمسارات الأطول من قمة بداية معينة في DAGs في الوقت الخطي عن طريق معالجة القمم بترتيب طوبولوجي، وحساب طول المسار لكل رأس ليكون الحد الأدنى أو الأقصى للطول الذي تم الحصول عليه عبر أي من حوافه الواردة.[15] في المقابل، بالنسبة إلى الرسوم البيانية التعسفية، قد يتطلب أقصر مسار خوارزميات أبطأ مثل خوارزمية Dijkstra أو خوارزمية Bellman-Ford ، ومن الصعب العثور على أطول المسارات في الرسوم البيانية التعسفية.[16] [17]

التطبيقات[عدل]

الجدولة

تمثيلات الرسوم البيانية غير الدورية الموجهة للطلبات الجزئية لها تطبيقات عديدة في جدولة أنظمة المهام مع قيود الترتيب. فئة مهمة من المشاكل من هذا النوع تتعلق بمجموعات الكائنات التي تحتاج إلى تحديث، مثل خلايا جدول البيانات بعد تغيير إحدى الخلايا، أو ملفات الكائن لجزء من برنامج الكمبيوتر بعد أن تم تعديل كود المصدر الخاص به. تغير. في هذا السياق، يمثل الرسم البياني التبعية رسمًا بيانيًا له رأس لكل كائن يتم تحديثه، وحافة تربط بين كائنين كلما احتاج أحدهما إلى التحديث قبل الآخر. تسمى الدورة في هذا الرسم البياني التبعية الدائرية، وهي غير مسموح بها عمومًا، لأنه لن تكون هناك طريقة لجدولة المهام المتضمنة في الدورة باستمرار. تشكل الرسوم البيانية التبعية بدون تبعيات دائرية DAGs.

على سبيل المثال، عندما تتغير خلية واحدة في جدول البيانات، من الضروري إعادة حساب قيم الخلايا الأخرى التي تعتمد بشكل مباشر أو غير مباشر على الخلية التي تم تغييرها. بالنسبة لهذه المشكلة، فإن المهام المراد جدولتها هي عمليات إعادة حساب قيم الخلايا الفردية في جدول البيانات. تنشأ التبعيات عندما يستخدم تعبير في خلية ما قيمة من خلية أخرى. في مثل هذه الحالة، يجب إعادة حساب القيمة المستخدمة قبل التعبير الذي يستخدمها. يسمح الترتيب الطوبولوجي لرسم بياني التبعية، واستخدام هذا الترتيب الطوبولوجي لجدولة تحديثات الخلية، بتحديث جدول البيانات بأكمله بتقييم واحد فقط لكل خلية. [31] تظهر مشكلات مماثلة في ترتيب المهام في ملفات makefiles الخاصة بتجميع البرامج وجدولة التعليمات لتحسين برامج الكمبيوتر منخفضة المستوى.

مخطط PERT لمشروع يحتوي على خمسة معالم (مسماة 10-50) وست مهام (معنون A – F). هناك مساران حرجان ، ADF و BC..

يتم استخدام صيغة مختلفة إلى حد ما قائمة على DAG لقيود الجدولة من خلال تقنية تقييم ومراجعة البرنامج (PERT)، وهي طريقة لإدارة المشاريع البشرية الكبيرة التي كانت أحد التطبيقات الأولى لـ DAGs. في هذه الطريقة، تمثل رؤوس DAG معالم المشروع بدلاً من المهام المحددة التي يتعين القيام بها. بدلاً من ذلك، يتم تمثيل المهمة أو النشاط بحافة DAG ، التي تربط بين معلمين يمثلان بداية المهمة وإكمالها. يتم تمييز كل حافة من هذا القبيل بتقدير لمقدار الوقت الذي سيستغرقه فريق من العمال لأداء المهمة. يمثل أطول مسار في DAG هذا المسار الحرج للمشروع ، وهو المسار الذي يتحكم في إجمالي الوقت للمشروع. يمكن جدولة المعالم الفردية وفقًا لأطوال المسارات الأطول المنتهية عند الرؤوس.[18]

شبكات معالجة البيانات

يمكن استخدام الرسم البياني غير الدوري الموجه لتمثيل شبكة من عناصر المعالجة. في هذا التمثيل ، تدخل البيانات عنصر معالجة من خلال حوافها الواردة وتترك العنصر من خلال حوافه الصادرة.

على سبيل المثال ، في تصميم الدوائر الإلكترونية ، يمكن تمثيل الكتل المنطقية التوافقية الثابتة كنظام لا دوري من البوابات المنطقية التي تحسب وظيفة أحد المدخلات ، حيث يتم تمثيل مدخلات ومخرجات الوظيفة على أنها بتات فردية. بشكل عام ، لا يمكن استخدام مخرجات هذه الكتل كمدخلات ما لم يتم التقاطها بواسطة سجل أو عنصر حالة يحافظ على خصائصه غير الدورية.[19] مخططات الدوائر الإلكترونية إما على الورق أو في قاعدة بيانات هي شكل من أشكال الرسوم البيانية غير الدورية الموجهة باستخدام مثيلات أو مكونات لتشكيل مرجع موجه إلى مكون المستوى الأدنى. الدوائر الإلكترونية نفسها ليست بالضرورة غير دورية أو موجهة.

تصف لغات برمجة تدفق البيانات أنظمة العمليات على تدفقات البيانات ، والوصلات بين مخرجات بعض العمليات ومدخلات البعض الآخر. يمكن أن تكون هذه اللغات ملائمة لوصف مهام معالجة البيانات المتكررة ، حيث يتم تطبيق نفس مجموعة العمليات المرتبطة دوريًا على العديد من عناصر البيانات. يمكن تنفيذها كخوارزمية متوازية يتم فيها تنفيذ كل عملية من خلال عملية متوازية بمجرد أن تصبح مجموعة أخرى من المدخلات متاحة لها.[20]

في المترجمين ، يمكن تمثيل رمز الخط المستقيم (أي تسلسل العبارات بدون حلقات أو فروع شرطية) بواسطة DAG الذي يصف مدخلات ومخرجات كل من العمليات الحسابية التي يتم إجراؤها داخل الكود. هذا التمثيل يسمح للمترجم بأداء حذف التعابير الفرعية بكفاءة. في مستوى أعلى من تنظيم الكود ، ينص مبدأ التبعيات غير الدورية على أن التبعيات بين الوحدات أو مكونات نظام برمجيات كبير يجب أن تشكل رسمًا بيانيًا لا دوريًا موجهًا.

الهياكل السببية

الرسوم البيانية التي تمثل فيها الرؤوس أحداثًا تحدث في وقت محدد ، وحيث تكون الحواف دائمًا نقطة من قمة الزمن المبكر إلى قمة الوقت المتأخر للحافة ، تكون بالضرورة موجَّهة وغير دورية. يتبع عدم وجود دورة لأن الوقت المرتبط بالرأس يزداد دائمًا كلما اتبعت أي مسار في الرسم البياني حتى لا يمكنك أبدًا العودة إلى قمة على مسار. هذا يعكس حدسنا الطبيعي بأن السببية تعني أن الأحداث لا يمكن أن تؤثر إلا على المستقبل ، ولا تؤثر أبدًا على الماضي ، وبالتالي ليس لدينا حلقات سببية. مثال على هذا النوع من الرسم البياني غير الدوري الموجه هو تلك التي تمت مواجهتها في نهج المجموعة السببية للجاذبية الكمية على الرغم من أن الرسوم البيانية التي تم النظر فيها في هذه الحالة مكتملة بشكل عابر. في مثال محفوظات الإصدار ، يرتبط كل إصدار من البرنامج بوقت فريد ، وعادةً ما يكون الوقت الذي تم فيه حفظ الإصدار أو الالتزام به أو إصداره. بالنسبة إلى الرسوم البيانية للاقتباس ، يتم نشر المستندات في وقت واحد ويمكن أن تشير فقط إلى المستندات القديمة.

في بعض الأحيان لا ترتبط الأحداث بوقت مادي معين. شريطة أن يكون لأزواج الأحداث علاقة سببية بحتة ، أي أن الحواف تمثل العلاقات السببية بين الأحداث ، سيكون لدينا رسم بياني لا دوري موجه.[21] على سبيل المثال ، تمثل شبكة بايز نظامًا للأحداث الاحتمالية كرؤوس في الرسم البياني غير الدوري الموجه ، حيث يمكن حساب احتمالية وقوع حدث من احتمالات أسلافها في DAG. في هذا السياق ، فإن الرسم البياني الأخلاقي لـ DAG هو الرسم البياني غير المباشر الذي تم إنشاؤه عن طريق إضافة حافة (غير موجهة) بين جميع الآباء من نفس الرأس (تسمى أحيانًا الزواج)، ثم استبدال جميع الحواف الموجهة بحواف غير موجهة. هناك نوع آخر من الرسم البياني له بنية سببية مماثلة وهو مخطط التأثير ، حيث تمثل رؤوسه إما قرارات يجب اتخاذها أو معلومات غير معروفة ، وتمثل حوافها تأثيرات سببية من رأس إلى آخر. في علم الأوبئة ، على سبيل المثال ، غالبًا ما تُستخدم هذه الرسوم البيانية لتقدير القيمة المتوقعة من الخيارات المختلفة للتدخل.[22] والعكس صحيح أيضا. في أي تطبيق يتم تمثيله بواسطة رسم بياني لا دوري موجه ، يوجد هيكل سببي ، إما ترتيب صريح أو وقت في المثال أو ترتيب يمكن اشتقاقه من بنية الرسم البياني. يتبع هذا لأن جميع الرسوم البيانية غير الدورية الموجهة لها ترتيب طوبولوجي ، أي أن هناك طريقة واحدة على الأقل لترتيب الرؤوس بحيث تشير جميع الحواف في نفس الاتجاه على طول هذا الترتيب.

علم الأنساب وتاريخ الإصدار

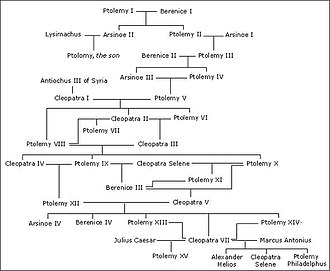
يمكن النظر إلى الأشجار العائلية على أنها رسوم بيانية غير دورية موجهة ، مع رأس لكل فرد من أفراد الأسرة وحافة لكل علاقة بين الوالدين والطفل. على الرغم من الاسم ، فإن هذه الرسوم البيانية ليست بالضرورة أشجارًا بسبب إمكانية الزواج بين الأقارب (لذا فإن الطفل له سلف مشترك من جهة الأم والأب) مما يتسبب في انهيار النسب. الرسوم البيانية للنسب الأمومي (علاقات «الأم» بين النساء) والنسب الأبوي (علاقات «الأب» بين الرجال) هي أشجار ضمن هذا الرسم البياني. نظرًا لأنه لا يمكن لأحد أن يصبح أسلافه ، فإن أشجار العائلة غير دورية.

شجرة عائلة سلالة البطالمة ، مع العديد من الزيجات بين الأقارب مما تسبب في انهيار النسب

]]

للسبب نفسه ، يحتوي تاريخ إصدار نظام التحكم في المراجعة الموزعة ، مثل Git ، بشكل عام على بنية الرسم البياني غير الدوري الموجه ، حيث يوجد رأس لكل مراجعة وحافة تربط أزواج المراجعات التي كانت مشتقة مباشرة من بعضها البعض. هذه ليست أشجارًا بشكل عام بسبب عمليات الدمج.

في العديد من الخوارزميات العشوائية في الهندسة الحسابية ، تحتفظ الخوارزمية بسجل DAG يمثل تاريخ إصدار بنية هندسية على مدار سلسلة من التغييرات في الهيكل. على سبيل المثال ، في خوارزمية تدريجية عشوائية لتثليث Delaunay ، يتغير التثليث عن طريق استبدال مثلث واحد بثلاثة مثلثات أصغر عند إضافة كل نقطة ، وعن طريق عمليات «قلب» التي تستبدل أزواج المثلثات بزوج مختلف من المثلثات. يحتوي سجل DAG لهذه الخوارزمية على رأس لكل مثلث تم إنشاؤه كجزء من الخوارزمية ، والحواف من كل مثلث إلى المثلثين أو المثلثات الثلاثة الأخرى التي تحل محله. تسمح هذه البنية بالإجابة على استعلامات موقع النقطة بكفاءة: للعثور على موقع نقطة استعلام q في تثليث Delaunay ، اتبع مسارًا في السجل DAG ، في كل خطوة ، انتقل إلى المثلث البديل الذي يحتوي على q. يجب أن يكون المثلث الأخير الذي يتم الوصول إليه في هذا المسار هو مثلث Delaunay الذي يحتوي على q.

الرسوم البيانية للاقتباس

في الرسم البياني للاقتباس ، تكون الرؤوس عبارة عن مستندات بتاريخ نشر واحد. تمثل الحواف الاقتباسات من ببليوغرافيا وثيقة ما إلى وثائق أخرى سابقة بالضرورة. يأتي المثال الكلاسيكي من الاستشهادات بين الأوراق الأكاديمية كما ورد في مقال «شبكات الأوراق العلمية» عام 1965 بقلم ديريك جيه دي سولا برايس الذي استمر في إنتاج النموذج الأول لشبكة الاستشهادات ، نموذج السعر. في هذه الحالة ، يكون عدد الاقتباسات لورقة ما هو مجرد درجة في الرأس المقابل لشبكة الاقتباس. هذا مقياس مهم في تحليل الاقتباس. تقدم أحكام المحكمة مثالاً آخر حيث يدعم القضاة استنتاجاتهم في قضية واحدة من خلال استدعاء قرارات سابقة أخرى صدرت في قضايا سابقة. يتم تقديم مثال أخير عن طريق براءات الاختراع التي يجب أن تشير إلى حالة التقنية الصناعية السابقة ، وبراءات الاختراع السابقة ذات الصلة بمطالبة البراءة الحالية. من خلال مراعاة الخصائص الخاصة للرسوم البيانية الحلقية الموجهة ، يمكن للمرء تحليل شبكات الاستشهاد بتقنيات غير متوفرة عند تحليل الرسوم البيانية العامة التي تم النظر فيها في العديد من الدراسات باستخدام تحليل الشبكة. على سبيل المثال ، يعطي الاختزال المتعدي رؤى جديدة حول توزيعات الاقتباسات الموجودة في التطبيقات المختلفة ، مع إبراز الاختلافات الواضحة في آليات إنشاء شبكات الاستشهادات في سياقات مختلفة. أسلوب آخر هو تحليل المسار الرئيسي ، والذي يتتبع روابط الاقتباس ويقترح سلاسل الاقتباس الأكثر أهمية في رسم بياني للاقتباس معين.

نموذج السعر بسيط للغاية بحيث لا يمكن أن يكون نموذجًا واقعيًا لشبكة الاستشهادات ، ولكنه بسيط بما يكفي للسماح بالحلول التحليلية لبعض خصائصها. يمكن العثور على العديد من هذه النتائج باستخدام النتائج المستمدة من النسخة غير الموجهة لنموذج السعر ، نموذج Barabási-Albert. ومع ذلك ، نظرًا لأن نموذج Price يعطي رسمًا بيانيًا لا دوريًا موجهًا ، فهو نموذج مفيد عند البحث عن الحسابات التحليلية للخصائص الفريدة للرسوم البيانية غير الدورية الموجهة. على سبيل المثال ، يتم قياس طول أطول مسار ، من العقدة رقم n المضافة إلى الشبكة إلى العقدة الأولى في الشبكة.

ضغط البيانات

يمكن أيضًا استخدام الرسوم البيانية غير الدورية الموجهة كتمثيل مضغوط لمجموعة من المتواليات. في هذا النوع من التطبيقات ، يجد المرء DAG حيث تشكل المسارات التسلسلات المحددة. عندما تشترك العديد من التسلسلات في نفس التتابعات اللاحقة ، يمكن تمثيل هذه التسلسلات اللاحقة المشتركة بجزء مشترك من DAG ، مما يسمح للتمثيل باستخدام مساحة أقل مما قد يتطلبه سرد جميع التسلسلات بشكل منفصل. على سبيل المثال ، الرسم البياني للكلمات غير الدورية الموجه عبارة عن بنية بيانات في علوم الكمبيوتر مكونة من رسم بياني لا دوري موجه بمصدر واحد ومع حواف موضحة بأحرف أو رموز ؛ تمثل المسارات من المصدر إلى الأحواض في هذا الرسم البياني مجموعة من السلاسل ، مثل الكلمات الإنجليزية. يمكن تمثيل أي مجموعة من المتتاليات كمسارات في شجرة ، من خلال تشكيل رأس شجرة لكل بادئة في التسلسل وجعل أصل إحدى هذه الرؤوس يمثل التسلسل بعنصر أقل ؛ الشجرة التي تشكلت بهذه الطريقة لمجموعة من الخيوط تسمى trie. يوفر الرسم البياني للكلمات الحلقية الموجه مساحة على مثلث من خلال السماح للمسارات بالتباعد والالتحاق مرة أخرى ، بحيث يمكن تمثيل مجموعة من الكلمات التي لها نفس اللواحق المحتملة برأس شجرة واحد.

تحدث نفس فكرة استخدام DAG لتمثيل مجموعة من المسارات في مخطط القرار الثنائي ، وهي بنية بيانات قائمة على DAG لتمثيل الوظائف الثنائية. في الرسم التخطيطي للقرار الثنائي ، تتم تسمية كل رأس غير حوضي باسم متغير ثنائي ، ويتم تسمية كل حوض وكل حافة بالرقم 0 أو 1. قيمة الوظيفة لأي تعيين حقيقة للمتغيرات هي القيمة عند تم العثور على الحوض باتباع مسار ، بدءًا من رأس المصدر الفردي ، والذي يتبع الحافة الصادرة عند كل قمة غير مغسلة للحافة الصادرة المسمى بقيمة متغير هذا الرأس. تمامًا كما يمكن عرض الرسوم البيانية للكلمات غير الدورية الموجهة باعتبارها شكلًا مضغوطًا من المحاولات ، يمكن عرض مخططات القرار الثنائي على أنها أشكال مضغوطة من أشجار القرار التي توفر مساحة من خلال السماح للمسارات بالانضمام عندما تتفق على نتائج جميع القرارات المتبقية.

المراجع[عدل]

  1. ^ موفق دعبول؛ بشير قابيل؛ مروان البواب؛ خضر الأحمد (2018)، معجم مصطلحات الرياضيات (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، ص. 6، OCLC:1369254291، QID:Q108593221
  2. ^ Thulasiraman، K.؛ Swamy، M. N. S. (1992)، "5.7 Acyclic Directed Graphs"، Graphs: Theory and Algorithms، John Wiley and Son، ص. 118، ISBN:978-0-471-51356-8.
  3. ^ Bang-Jensen، Jørgen (2008)، "2.1 Acyclic Digraphs"، Digraphs: Theory, Algorithms and Applications، Springer Monographs in Mathematics (ط. 2nd)، Springer-Verlag، ص. 32–34، ISBN:978-1-84800-997-4.
  4. ^ Christofides، Nicos (1975)، Graph theory: an algorithmic approach، Academic Press، ص. 170–174.
  5. ^ Mitrani، I. (1982)، Simulation Techniques for Discrete Event Systems، Cambridge Computer Science Texts، Cambridge University Press، ج. 14، ص. 27، ISBN:9780521282826، مؤرشف من الأصل في 2022-01-05.
  6. ^ Kozen، Dexter (1992)، The Design and Analysis of Algorithms، Monographs in Computer Science، Springer، ص. 9، ISBN:978-0-387-97687-7، مؤرشف من الأصل في 2021-08-10.
  7. ^ Banerjee، Utpal (1993)، "Exercise 2(c)"، Loop Transformations for Restructuring Compilers: The Foundations، Springer، ص. 19، ISBN:978-0-7923-9318-4، مؤرشف من الأصل في 2022-01-05.
  8. ^ Bang-Jensen، Jørgen؛ Gutin، Gregory Z. (2008)، "2.3 Transitive Digraphs, Transitive Closures and Reductions"، Digraphs: Theory, Algorithms and Applications، Springer Monographs in Mathematics، Springer، ص. 36–39، ISBN:978-1-84800-998-1، مؤرشف من الأصل في 2022-06-09.
  9. ^ Jungnickel، Dieter (2012)، Graphs, Networks and Algorithms، Algorithms and Computation in Mathematics، Springer، ج. 5، ص. 92–93، ISBN:978-3-642-32278-5، مؤرشف من الأصل في 2022-06-09.
  10. ^ McKay، B. D.؛ Royle، G. F.؛ Wanless، I. M.؛ Oggier، F. E.؛ Sloane، N. J. A.؛ Wilf، H. (2004)، "Acyclic digraphs and eigenvalues of (0,1)-matrices"، Journal of Integer Sequences، ج. 7، مؤرشف من الأصل في 2022-11-30, Article 04.3.3.
  11. ^ Sedgewick، Robert؛ Wayne، Kevin (2011)، "4,2,25 Unique topological ordering"، Algorithms (ط. 4th)، Addison-Wesley، ص. 598–599، ISBN:978-0-13-276256-4، مؤرشف من الأصل في 2021-04-12.
  12. ^ Bender، Edward A.؛ Williamson، S. Gill (2005)، "Example 26 (Linear extensions – topological sorts)"، A Short Course in Discrete Mathematics، Dover Books on Computer Science، Courier Dover Publications، ص. 142، ISBN:978-0-486-43946-4، مؤرشف من الأصل في 2021-08-10.
  13. ^ Robinson، R. W. (1973)، "Counting labeled acyclic digraphs"، في Harary، F. (المحرر)، New Directions in the Theory of Graphs، Academic Press، ص. 239–273. See also Harary، Frank؛ Palmer، Edgar M. (1973)، Graphical Enumeration، Academic Press، ص. 19، ISBN:978-0-12-324245-7.
  14. ^ Picard، Jean-Claude (1976)، "Maximal closure of a graph and applications to combinatorial problems"، قالب:Ill-WD2Management Science، ج. 22، ص. 1268–1272، DOI:10.1287/mnsc.22.11.1268، MR:0403596.
  15. ^ Cormen et al. 2001, Section 24.2, Single-source shortest paths in directed acyclic graphs, pp. 592–595.
  16. ^ Cormen et al. 2001, Sections 24.1, The Bellman–Ford algorithm, pp. 588–592, and 24.3, Dijkstra's algorithm, pp. 595–601.
  17. ^ Cormen et al. 2001, p. 966.
  18. ^ Wang، John X. (2002)، What Every Engineer Should Know About Decision Making Under Uncertainty، CRC Press، ص. 160، ISBN:978-0-8247-4373-4، مؤرشف من الأصل في 2022-01-05.
  19. ^ Sapatnekar، Sachin (2004)، Timing، Springer، ص. 133، ISBN:978-1-4020-7671-8، مؤرشف من الأصل في 2022-06-09.
  20. ^ Dennis، Jack B. (1974)، "First version of a data flow procedure language"، Programming Symposium، Lecture Notes in Computer Science، ج. 19، ص. 362–376، DOI:10.1007/3-540-06859-7_145، ISBN:978-3-540-06859-4.
  21. ^ Touati، Sid؛ de Dinechin، Benoit (2014)، Advanced Backend Optimization، John Wiley & Sons، ص. 123، ISBN:978-1-118-64894-0، مؤرشف من الأصل في 2022-06-09.
  22. ^ Garland، Jeff؛ Anthony، Richard (2003)، Large-Scale Software Architecture: A Practical Guide using UML، John Wiley & Sons، ص. 215، ISBN:9780470856383، مؤرشف من الأصل في 2021-04-12.
مجلوبة من «https://ar.wikipedia.org/w/index.php?title=بيان_موجه_خال_من_الحلقات&oldid=66611422»